Le proto est fini. Youpiiiiiiiii !!!!
Alors, comme y'a pas de raison que je n'y aille pas non plus de mon petit graphique de résultats qui déchire, voilà :
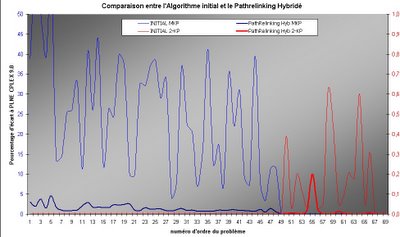
Il s'agit de résultats concernant la résolution approchée de problèmes de sacs à dos difficiles.
- en bleu : des multi contraints (plusieurs dizaines de contraintes)
- en rouge : des bi contraints corrélés
ainsi que :
- en fin : ce que donnait l'algorithme initial
- en gras, ce que donne la combinaison de :
- l’algorithme initial amélioré (Algorithme de sous gradient projeté)
- deux heuristiques d’amélioration supplémentaire (PL et Montée)
- une métaheuristique (Pathrelinking avec fusion)
Ce dont on peut s'apercevoir à prime abord, c'est que pour les multi contraints, l'algorithme d'origine donne des résultats par rapport à la valeur calculée initialement par CPLEX 9.0 qui varient entre 10 et 45% quand ma version donne des résultats stables aux environs d' à peine quelques pourcents. Pour les problèmes bicontraints, quand l'algorithme initial donne des solutions approchées de l'ordre de 0,5%, j'en suis pour ma part à 0,0.. % ;-))))
Ca, c'est pour la métaheuristique qui manipule des populations de solutions. Il y a d'autres résultats avec une autre métaheuristique (qui, elle, manipule des voisinages de solutions) qui donne également de bons résultats. La suite dans quelques jours...


10 Comments:
justement, c'est ça, un des problèmes à résoudre...
J'ai tout compris mon poussin ... enfin presque ;o) !
c'est bien mon chéri, maintenant y a plus qu'à prendre ton beau petit stylo plume mont blanc et à rédiger...
euh non ça c'était à l'ancienne...
euh tu n'as plus qu'à prendre ton "latec" (si j'ai bien compris) ;-)) et à rédiger ET PLUS VITE QUE CA CAR JE VEUX PARTIR EN VACANCES EN WEEK END AU SKI A LA MONTAGNE EN SUISSE A VENISE DU JOUR AU LENDEMAIN enfin bon tu m'as comprise....
allez zou au travail...
moi je vais me mater un petit fimm pendant que tu travailles;-))))
courage
Bravo ! C'est toujours une sensation extra quand on arrive à un résultat comme ça.
Mon extériorisation de la chose, c'est comme ça : je me frotte les mains très fort, et je suis tout content !
On y comprend pas grand chose quand même : que donne ta méthode par rapport à ton CPLEX?
On y comprend pas grand chose quand même : que donne ta méthode par rapport à ton CPLEX?
CPLEX est une référence COMMERCIALE. Et ça reste aussi une boite noire...
Moi, je suis libre...
Mais le but du jeu n'est pas de se comparer à CPLEX. D'une part parce que je travaille en terme de résolution approchée, pas CPLEX, et d'autre part, je devais réfléchir à "comment améliorer la version initiale du sous gradient, en lui insérant, éventuellement, une métaheuristique"
On peut très bien faire marcher CPLEX en terme de résolution approchée. Il suffit de l'arrêter à un moment donné et de regardé sa solution courante... Certes, cette solution n'est pas forcément optimale mais elle est souvent bonne
oui, oui, tout à fait.
Mais ce n'est pas le but.
Sur des instances difficiles, difficiles et difficiles, la résolution exacte n'a pas bcp de sens.
je m'explique :
le premier "difficile" provient du fait que je travaille sur des pb np-complets.
le deuxième "difficile", sur le fait que les instances sont travaillées (elle sont dites fortement corrélées [strongly corralated]) pour être en moyenne bcp plus difficiles que des instances aléatoires.
Enfin, le troisième "difficile" vient du fait que parmi les précédentes instances (il y en avait environ 400 provenant pour tout ou partie de la OR Library) je n'ai gardé que les 70 plus difficiles.
Bien. Mais en fait, les valeurs données par CPLEX ne sont pas forcément les valeurs optimales du pb : en effet, j'ai arrêté CPLEX au bout de 900s, ce qui donne déjà une très bonne idée de l'optimalité. De temps en temps, CPLEX est à l'optimal, mais il ne le sait pas encore. Certains problèmes, sur un gros serveur de calculs, ont demandé plus de 15h de clacul intensifs...
De plus, on travaille sur des pb de petites tailles : quelques centaines de variables, quelques dizaines de contraintes... J'ai généré des pb de très grande taille (plusieurs centaines de contraintes, plusieurs dizaines de milliers de variables...)
Bref, même si CPLEX est bon, voire même excellent, il ne s'agit pas de laisser à CPLEX (commerciale boite noire) la primeur de tout résultat, d'où l'idée de développer d'autres algorithmes. Le mien montre que sur des problèmes extrêmement difficiles, quand on ne dispose que d'un quart d'heure de calcul (exemple de l'aéroport : recalculs en fonction d'aléa, calcul à faire dans l'urgence), mon algo vaut CPLEX. Et mon algo est gratuit. pas CPLEX.
t'es le plus fort mon chou!!!!
mais bon maintenant va falloir ramener des pepettes à la maison!!
et mon aston martin, je vais attendre jusqu'à quand!!!
Enregistrer un commentaire
<< Home